Binary search program in C using an array

---

Introduction of Binary Search Program in C Using Array

Binary Search Program in C Using Array is one of the most efficient search algorithms used to find an element in a sorted array. Unlike linear search, which checks each element sequentially, binary search significantly reduces the number of comparisons by repeatedly dividing the search interval in half. This makes binary search particularly useful when working with large datasets.

What is Binary Search?

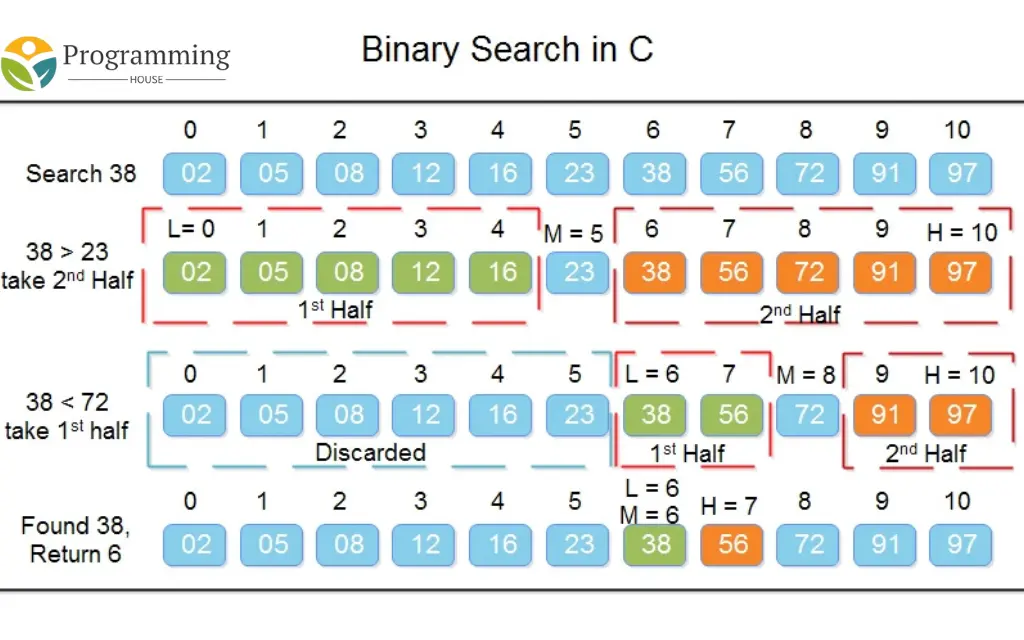
Binary search is a separate-and-overcome treasure that finds the position of a goal value within a sorted array. The algorithm entirety by matching the goal value to the middle detail of the array. If the goal advantage matches the middle part, its position is returned. If the target value is less than the middle element, the search continues in the left half of the array; alternatively, it resumes in the right half. This process repeats as far as the target value is erect or the subarray reduces to nothing.

How Binary Search Works

Here’s how binary search works step-by-step:

1. Initial Setup: Define the lower bound (low) as the first index of the array and the upper bound (high) as the last index.
2. Find the Midpoint: Calculate the midpoint index (mid) using the formula: [
   \text{mid} = \text{low} + \frac{(\text{high} – \text{low})}{2}
   ]
3. Compare the Midpoint Element:

• If the midpoint element equals the target value, the search is successful, and the index of the midpoint is returned.
• If the midpoint element is greater than the target value, update high to mid - 1 and repeat the search on the left half.
• If the midpoint element is less than the target value, update low to mid + 1 and repeat the search on the right half.

1. Repeat until low is greater than high. If the target is not found, return an indication (usually -1) that the element is not present in the array.

Advantages of Binary Search Program in C Using Array

• Time Complexity: O(log n), which is much faster compared to linear search’s O(n), especially for large arrays.
• Space Complexity: O(1), as it requires a constant amount of extra space.

Limitations of Binary Search

• The array must be sorted; otherwise, the search results will be incorrect.
• The algorithm works only with direct access data structures like arrays and not with linked lists.

Binary Search Implementation in C

Below is a complete implementation of the binary search algorithm in C using an array.

#include <stdio.h>

// Function prototype
int binarySearch (int array[], int low, int high, int target);

// Main function
int main() {
    int array[] = {2, 4, 7, 10, 15, 18, 20, 24, 30}; // Sorted array
    int size = sizeof(array) / sizeof(array[0]);     // Calculate size of array
    int target;

    // Prompt the user to enter the target value
    printf("Enter the number you want to search for: ");
    scanf("%d", &target);

    // Perform binary search
    int result = binarySearch(array, 0, size - 1, target);

    // Check if the target is found or not
    if (result != -1) {
        printf("Element %d found at index %d.\n", target, result);
    } else {
        printf("Element %d not found in the array.\n", target);
    }

    return 0;
}

// Binary Search Function
int binarySearch(int array[], int low, int high, int target) {
    while (low <= high) {
        // Calculate the midpoint
        int mid = low + (high - low) / 2;

        // Check if the target is at the midpoint
        if (array[mid] == target) {
            return mid; // Target found
        }

        // If target is less than the midpoint element, search in the left half
        if (array[mid] > target) {
            high = mid - 1;
        } 
        // If target is greater, search in the right half
        else {
            low = mid + 1;
        }
    }

    return -1; // Target not found
}

Explanation of the Code

1. Input and Setup: The program initializes a sorted array and prompts the user to input the target value they want to search for.
2. Binary Search Function:

• The function binarySearch accepts the array, the lower (low) and upper (high) bounds of the array, and the target value to be searched.
• A while loop runs as long as low is less than or equal to high. Within this loop, the midpoint is calculated using the formula mid = low + (high - low) / 2 to avoid potential overflow errors.
• If the element at the midpoint matches the target, the index is returned.
• If the target is less than the midpoint element, high is adjusted to search in the left subarray.
• If the target is greater, low is adjusted to search in the right subarray.
• If the element is not found, the function returns -1.

Dry Run of the Code

Let’s dry run the program with an example array and target value to see how it works.

Example:

• Array: {2, 4, 7, 10, 15, 18, 20, 24, 30}
• Target: 18

Steps:

1. Initial low = 0, high = 8, midpoint mid = 4 (value = 15).
2. Since 18 > 15, update low = mid + 1 = 5.
3. New mid = 6 (value = 20).
4. Since 18 < 20, update high = mid - 1 = 5.
5. New mid = 5 (value = 18). Match found, return index 5.

Applications of Binary Search

• Searching in large databases: Ideal for applications where data is sorted, such as telephone directories or search engines.
• Algorithm optimization: Many algorithms, including those for machine learning and data compression, use binary search for optimization.
• Problem-solving: Useful in problems where conditions change based on ranges, such as finding square roots or the next greater element.

Conclusion

Binary search is an effective search invention that intensely reduces the number of contrastings wanted to find an component in a sifted array. Understanding allure active system and decent exercise in C can considerably improve your logical abilities, particularly when handling big datasets. Mastering twofold search opens dismissal from responsibility to more complex dossier forms and algorithms that depend fast search capabilities.

Practice Problems

1. Implement binary search on an array of strings and sort the array alphabetically.
2. Modify the binary search algorithm to find the first occurrence of a repeated element.
3. Use binary search to implement a dictionary feature where you search for words and their definitions.

---